n개 중 중복을 허용하고 r개를 선택하여 꺼내는 조합의 총수를 계산합니다.

전체 수 (n 개)와 선택한 수 (r 개)를 입력하고 "조합 계산"버튼을 클릭하면 n 개 중에서 중복을 허용하고 r 개를 선택하여 꺼내는 조합의 총수를 계산하여 표시합니다.

또한 조합의 총 수를 구하는 계산 방법도 표시합니다.

전체 수과 선택한 수은 10,000까지의 양의 정수로 입력하세요.

조합이란, 구별 가능한 다른 것들 중에서, 몇 가지를 선택해 꺼내는 것입니다.

중복을 용서하고 선택하여 꺼낸 조합을 조합이라고 합니다.

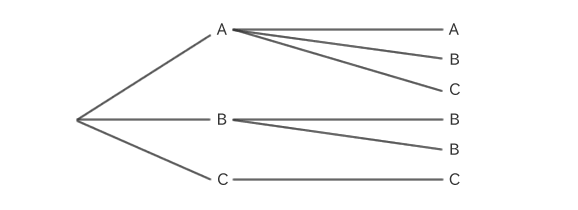
예를 들어, A, B, C의 3개의 알파벳 중에서 2개를 선택한다고 가정합니다.

같은 것을 여러 번 선택할 수도 있으므로, 이 때의 선택 방법은, “AA, AB, AC, BB, BC, CC”의 6가지가 됩니다.

조합에서는 순열과 달리 순서를 생각하지 않기 때문에, AB와 BA라고 하는 정렬해 같게 되는 조합은 1개로서 생각합니다.

A, B, C에서 2개를 선택한 경우의 조합을 수형도로 하면 이와 같이 됩니다.

중복조합의 총 수를 계산하려면 원과 구분 기호를 사용하여 생각합니다.

예를 들면, A, B, C의 3개의 알파벳이 있고, 이 중에서 4개를 선택해 조합을 생각한다고 합니다.

선택하는 4개의 알파벳을 원(〇)으로 하고, 알파벳의 종류가 3종류이므로 칸막이(|)를 2개 준비해 늘어놓습니다.

원과 분할을 나란히 하고, 분할의 왼쪽으로부터 ABC로 합니다.

예를 들어, 〇〇｜〇｜〇의 경우는, AABC의 조합이 됩니다.또, 〇｜｜〇〇〇의 경우는, ACCC의 조합이 됩니다.

이 원과 분할의 순열의 총수가, 중복조합의 총수가 됩니다.

원과 구분의 순열의 총수는 6!로, 원과 구분은 각각 구별이 없기 때문에 (4! × 2!)로 나눕니다.

따라서 총 조합 수는 6!4!2! = 15입니다.

따라서 n개에서 r개를 중복을 허용하여 선택하여 꺼낸 조합의 총수는 (r+n−1)!r!(n−1)!로 계산할 수 있습니다.